[TS] 시계열 데이터 정리와 기본 개념

이 글은 책 '실전 시계열 분석'을 재구성하여 작성되었습니다.

책링크

실전 시계열 분석

---

Data Handling

 

1. Missing value

 

 

시계열만이 아닌 대부분의 빅데이터에는 결측치가 존재하는 경우가 많습니다. 다양한 이유에서 값이 누락되는 경우가 발생하는 것이죠. 간단한 이유로는 금융사는 고객의 개인정보를 암호화하여 일정한 형태로 저장하는 경우도 있지만 공개되는 데이터에는 값을 제외하는 경우도 많습니다. 이런 다양한 이유로 데이터에 결측치가 발생하는 것이죠.

결측치를 제거하고 데이터를 처리해도 되지만 반드시 괜찮다는 보장은 할 수 없습니다. 만약 결측치가 애매한 비율로 존재하지만 꽤 중요한 정보인 경우에는 결측치가 있는 attribute를 살려야 하기 때문이죠. 그래서 통계학적 방법에는 다양한 결측치 처리 방식이 연구되었습니다.

 

1) 대치법 (Imputation)

 

- 포워드 필 (Forward Fill) : 결측치의 직전 값으로 결측치를 채우는 방법

 

붉은색 점선은 forward fill 그래프이고 역삼각형은 포워드 필로 채워진 데이터

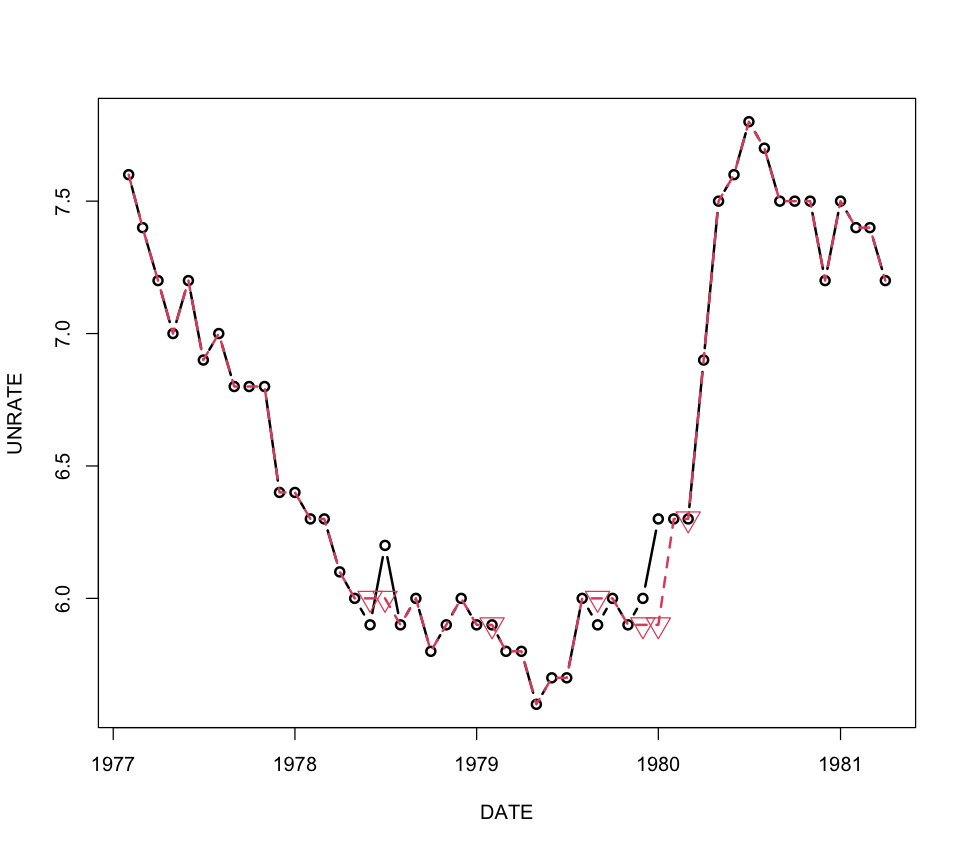
그래프에서 볼 수 있듯이 포워드 필은 원본 데이터의 성향을 띄는 경향이 강합니다. 직전 값으로 결측치를 채우는 방식을 포워드 필, 직후의 값으로 결측치를 채우는 것을 백워드 필 (Backward fill)이라고 합니다. 백워드 필은 일반적으로 미래보다 과거를 채우는 게 더 의미가 있는 경우에 사용합니다.

포워드 필은 계산이 간단하다는 장점이 있고 직전값을 바로 활용하하기 때문에 실시간 스트리밍 데이터에 유리하다는 장점이 있습니다. 그리고 바로 직전 값을 쓰므로 대치작업이 수월하고 코드도 간단합니다.

책에는 R코드로 작성되어 있지만 파이썬으로 변환하는 작업을 하고 있기 때문에 파이썬코드를 올려드리겠습니다. 원본 코드는 깃허브 링크를 참조해주세요.

 

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import interpolate

# forward fill
rand_unemp['impute.ff'] = rand_unemp.UNRATE.fillna(method='ffill')
bias_unemp['impute.ff'] = bias_unemp.UNRATE.fillna(method='ffill')

fig, ax = plt.subplots(figsize=(12,7))
# origianl graph
sns.scatterplot(data=unemp[350:400], x='DATE', y='UNRATE')
sns.lineplot(data=unemp[350:400], x='DATE', y='UNRATE')
# random missing value graph
sns.lineplot(data=rand_unemp[350:400], x='DATE', y='impute.ff')
sns.scatterplot(data=rand_unemp[350:400][rand_unemp['rpt'] == True], x='DATE', y='impute.ff', marker='v', s=100)

plt.show()

데이터를 판다스의 read_csv 모듈을 활용해서 적당하게 불러오고 일부러 결측치를 만들었습니다. 

코드 참조는 forward fill 주석 부분을 확인하시면 됩니다. 파이썬에는 편리하게 fillna() 메소드가 있습니다. 내부에 ffill을 파라미터로 넘겨주면 자동으로 포워드 필의 형태를 띕니다.

 

 

- 이동평균 (moving average) : 최근 과거의 여러 시간대의 내용을 활용하여 채우는 방법 (평균, 중앙값 등을 활용)

 

빨간 선은 사전관찰이 있는 경우, 초록 선은 사전관찰이 없는 경우입니다.

이동평균을 사용할 때는 사전관찰이 들어가는 경우와 들어가지 않는 경우를 구분해서 알아야합니다. 주어진 정보를 이용해서 통계값으로 대치하기 때문이죠. 그래서 사전관찰이 적용되는 경우와 그렇지 않은 경우를 구분해서 확인해봅시다. 정보가 부족할수록 평균치의 오차가 커지기 때문에 실제 그래프와 차이가 발생합니다. 그래서 사전관찰의 여부를 반드시 생각해야합니다.

 

# moving average
rand_unemp['impute.rm.nolookahead'] = rand_unemp[['UNRATE']].rolling(3, min_periods=1).mean()
bias_unemp['impute.rm.nolookahead'] = bias_unemp[['UNRATE']].rolling(3, min_periods=1).mean()

rand_unemp['impute.rm.lookahead'] = rand_unemp[['UNRATE']].rolling(3, min_periods=1, center=True).mean()
bias_unemp['impute.rm.lookahead'] = bias_unemp[['UNRATE']].rolling(3, min_periods=1, center=True).mean()

fig, ax = plt.subplots(figsize=(12,7))
# origianl graph
sns.scatterplot(data=unemp[49:108], x='DATE', y='UNRATE')
sns.lineplot(data=unemp[49:108], x='DATE', y='UNRATE', label='original')
# random missing value graph
sns.lineplot(data=rand_unemp[49:108], x='DATE', y='impute.rm.nolookahead', label='no lookahead')
sns.scatterplot(data=rand_unemp[49:108][rand_unemp['rpt'] == True], x='DATE', y='impute.rm.nolookahead', marker='v', s=100)
sns.lineplot(data=rand_unemp[49:108], x='DATE', y='impute.rm.lookahead', color='green', label='lookahead')
sns.scatterplot(data=rand_unemp[49:108][rand_unemp['rpt'] == True], x='DATE', y='impute.rm.lookahead', marker='x', s=100, color='green')

plt.legend()
plt.show()

 

---

 

2) 보간법 (interpolation) : 전체 data를 기하학적 행동에 제한하여 결측치를 결정

 

대표적인 보간법으로는 선형보간법(linear interpolation)이 있습니다. 선형보간법은 결측치가 주변 데이터에 대해서 선형적인 일관성을 갖게됩니다. 상황에 따라 선형성을 지니는게 원본 데이터와 근접하게 나오는 경우도 많습니다. 그래서 이런 보간법을 사용해서 결측치를 채웁니다. 이때 이동평균과 마찬가지로 과거, 미래 데이터의 활용 여부를 결정하는 것이 중요합니다.

미래 데이터를 활용하는 경우에는 사전관찰에 주의해줘야 합니다. 미래 데이터가 사용되면 선형성에 영향을 끼칠 수 있기 때문입니다. 

그래서 사전관찰이 데이터에 영향을 크게 미칠 수 있는지 확인을 반드시 해야합니다.

 

초록색은 spline interpolation, 빨간색은 liner interpolation

보간법은 데이터의 추세를 알고 있는 경우에는 이동평균보다 데이터를 더 잘 대치할 수 있습니다. 하지만 강수량, 수면 시간처럼 비선형적 추세를 갖는 데이터에는 적절하진 않습니다.

 

# linear interpolation
tmp1 = rand_unemp.set_index('DATE')
tmp2 = bias_unemp.set_index('DATE')
rand_unemp['impute.li'] = tmp1['UNRATE'].interpolate().values
bias_unemp['impute.li'] = tmp2['UNRATE'].interpolate().values

interpolation 메소드를 사용하면 간단하게 구현할 수 있습니다.

 

---

2. Sampling

 

데이터의 불규형이 발생하는 경우가 있습니다. 이런 경우에는 2가지 방식으로 데이터 균형을 맞출 수 있습니다.

다운샘플링과 업샘플링이 있습니다. 간단하게 다운샘플링부터 알아봅시다.

 

1) 다운샘플링 (down sampling) : 데이터의 빈도를 줄이는 것

 

데이터의 부분집합을 형성하는 방식입니다. 위에 사용한 결측치 샘플은 일부 데이터를 추출해서 만든 다운샘플링 데이터입니다.

다운샘플링은 다음과 같은 경우에 자주 이뤄집니다.

 

a) 원본 데이터의 시간 단위가 실용적이지 않는 경우

시간 단위가 너무 빈번하게 되는 경우에 다운 샘플링을 진행합니다. 만약 온도를 측정한 데이터가 초단위로 기록된 경우라면 불필요하게 많은 데이터가 기록되어 있습니다. 어떻게보면 세밀한 변화를 기록해서 더 좋은게 아닐까 싶은 생각을 할 수 있습니다. 하지만 데이터가 빈번하게 기록되어 있다는 것은 오차 빈도도 간격만큼 발생할 위험이 있다는 것입니다. 그래서 몇개의 데이터만 추출해서 데이터 자체를 감소할 필요가 있습니다.

 

b) 계절 주기의 특정 부분에 집중하는 경우

특정 계절에만 집중해서 데이터를 형성할 필요가 있습니다. 자연적인 것들, 사람의 행동, 많은 데이터들이 주기성을 갖는 경우가 많습니다. 이런 경우에는 전체 데이터에서 특정 주기 부분만 샘플링 할 필요가 있습니다.

 

c) 더 낮은 빈도의 데이터에 맞추는 경우

이 경우는 실제 사용되는 경우로는 훈련 데이터에 비해 테스트 데이터가 너무 작을 경우에 사용하는 방식입니다. 일반적으로는 data imblance가 큰 경우에 사용한다고 합니다. 하지만 단순히 데이터를 삭제하는 건 경향성을 중요시하는 시계열 데이터의 경향성을 깨트릴 수 있습니다. 그래서 데이터를 취합해서 다운샘플링을 진행해야합니다.

평균이나 합계를 구하는 과정일 수 있지만 나중 값에 더 가중치를 주는 가중치 평균같은 과정을 사용할 수도 있습니다.

 

---

 

2) 업샘플링 (up sampling) : 드물게 측정된 데이터를 더 조밀한 시간의 데이터로 형성

 

이름에서는 단순히 다운샘플링과 반대되는 것처럼 보이지만 실제로 단순한 반대개념은 아닙니다. 잘 생각해보면 조밀한 데이터를 줄여내는 과정은 실제로 자주 일어나는 상황입니다. 하지만 업샘플링은 실제로 측정한 것이 아닌 데이터를 얻어내는 과정입니다.

R의 시계열 패키지 XTS를 제작한 사람이 했던 말이 있습니다.

시계열을 낮은 주기에서 높은 주기로 바꿀 수는 없습니다. 예를 들어 데이터를 주간에서 일간으로, 일간에서 5분 단위로 변환하기 위해서는 마법과도 같은 능력이 필요합니다.

 

하지만 높은 빈도로 데이터를 레이블링 해야하는 경우는 필요합니다. 더 많은 레이블이 추가되는 것은 맞지만, 많은 정보가 추가되는 것은 아니라는 것을 알아야합니다.

 

a) 시계열이 불규칙한 상황

데이터의 시차보다 더 높은 빈도로 전체 데이터를 변환합니다. 이런 경우에는 결측치가 발생할 수 있으므로 결측치를 다루는 방식을 잘 활용해서 데이터를 생성해줘야 합니다.

 

b) 입력이 서로 다른 빈도로 샘플링된 상황

현재 보유한 데이터보다 더 높은 빈도를 요구하는 경우입니다.

두 데이터의 시간대를 동일하게 정렬해줘야 합니다. 이때 반드시 사전관찰을 주의해야 합니다. 지금까지 있는 데이터로만 추측을 한다면 안전한 샘플링이 되겠지만 사전관찰이 발생한다면 문제가 발생할 수도 있습니다.

 

---

3. Smoothing

 

Smoothing은 '데이터 평활'이라고 합니다.  평활이 필요한 이유로는 측정 오류, 너무 높게 튀는 측정치를 제거하는 데에 있습니다. 결측치를 처리할 때, 문제가 있는 데이터가 관여를 한다면 아주 작은 값 하나가 결측치에 영향을 주며 전체 경향을 해칠 수 있기 때문이죠.

시계열에서는 일반적으로 지수평활 (exponential smoothing)을 사용합니다. 

 

지수평활 (exponential smoothin)

시간성을 가진 데이터는 최근에 가까울수록 데이터의 가치가 높을 것이라 생각할 수 있습니다. 그리고 실제로도 영향이 있을 수도 있습니다. 그래서 이를 적용하고자 시간상 가까운 데이터에 가중치를 부여하여 시간적 특성을 살려주는 평활 방식입니다.

 

시간이 t일때 평활된 값을 $S_{t}$라고 할때, $S_{t}$의 식은 아래와 같습니다.

 

$$ S_{t} = d \times S_{t-1} + (1-d) \times x_{t} $$

 

이 식에 따르면 $S_{t-1} = d \times (d \times S{t-2} + (1-d) \times x_{t-1}) + (1-d) \times x_{t}$로 볼 수 있습니다.

이걸 토대로 $S_{t}$를 다시 정의하면 아래와 같이 정의됩니다.

 

$$S_{t} = d \times (d \times S_{t-2} + (1-d) \times x_{t-1}) + (1-d) \times x_{t} \\ = ( .... ) + d^{n} \times x_{t-n} + d^{n-1} \times x_{t-(n-1)} + ... + d \times x_{t-1}$$

 

식을 보면 알 수 있듯이 d가 0 ~ 1사이 값이하면 오래된 데이터일수록 0에 가까운 값이 곱해지면 해당 데이터가 영향을 줄 확률은 낮아집니다. 이때 d는 가중치라고 합니다.

이때 평활 요인인 $\alpha$가 존재합니다. $\alpha$가 클수록 현재 값에 가깝도록 더 빨리 갱신됩니다.

 

하지만 지수평활에도 단점은 존재합니다. 장기적인 추세의 데이터는 단순한 지수평활 예측을 잘하지 못합니다.

이런 경우에는 홀트의 방법이나 홀트-윈터스의 평활을 활용합니다.

지수쳥활만이 아닌 다른 평활 방법들도 있습니다. 칼만필터 (Kalman Filter), 뢰스(LOESS, locally estimated scatterplot smoothing) 가 있습니다. 칼만필터는 변동성이나 측정 오차 조합으로 데이터 평활을 합니다. 그리고 뢰스는 지역적으로 데이터를 평활하는 비모수적 방법입니다.

 

---

Seasonal Data

 

Seasonal data (계절성 데이터)

 

특정 행동의 빈도가 안정적으로 반복해서 나타나는 데이터를 계정성 데이터라고 합니다. 대체적으로 인간의 행동은 일일, 주간, 연간의 계절적 변화 경향성을 가집니다. 이를 분석할때, 산점도와 선 그래프를 활용하는데 두 방식에는 각자의 장점이 존재합니다.

 

 

좌측의 산점도는 원뿔형태의 데이터 분포가 바깥으로 향하게 보여줍니다. 변동성의 추세를 알기는 쉽지 않습니다. 하지만 편차, 분산이 증가한다는 것을 명확하게 알 수 있습니다.

우측의 선그래프는 계절적 변동의 추세를 확인하기 좋습니다. 배수적인 계절성의 변동 크기를 알 수 있다는 장점이 있습니다. 쉽게 말하면 1952년의 계절성 폭보다 1960년의 계절성 폭이 좀 더 배로 증가한 것을 알 수 있습니다.

 

 

데이터의 실제 분포, 추세(경향성), 계절성, 잔차를 한번에 보여주는 방법이 있습니다. 파이썬에는 statsmodel 라이브러리에 있는 seasonal_decompose 모듈이 있습니다.

 

from statsmodels.tsa.seasonal import seasonal_decompose

tmp = air.set_index('Date')
ts = tmp.Passengers
result = seasonal_decompose(ts, model='additive')


plt.rcParams['figure.figsize'] = [12, 8]
result.plot()
plt.show()

 

깃허브 코드 - https://github.com/cow-coding/ML-DL-Study/tree/master/Practical%20Time%20Series%20Analysis/Only%20Python