[Data Structure] Binary Search Tree (이진 탐색 트리)
Binary Search Tree (이진 탐색 트리)
이진 탐색 트리는 앞서서 배운 트리의 확장적인 형태라고 보면 편하다. 일반적인 이진 트리는 탐색의 기준이 없어서 특정 데이터를 찾으려면 모든 노드를 탐색해야한다.
하지만 이진 탐색 트리에서는 평균적으로 훨씬 빠른 시간에 탐색이 가능해진다.
Binary Search (이진 탐색)
우선 이진 탐색과 이진 탐색 트리를 구분해야 한다. 전자는 알고리즘의 일종이고 후자는 자료구조의 일종이다. 이진 탐색 트리의 원리를 알기 이전에 이진탐색의 원리를 알아야 한다.
이진 탐색은 간단하게 말하면 탐색 범위를 절반으로 줄여나가는 탐색이다. 바로 이전 포스트에서 말한 search table과 같다. 굳이 자세한 설명을 더 하진 않겠다.
이런 이진 탐색을 트리 형태로 구조화시키면 그게 이진 탐색 트리이다.
시간 복잡도
BST의 시간복잡도는 트리의 모양과 관련이 깊다. 기준값보다 큰 값을 우측으로, 작은 값을 좌측으로 보내기 때문에 특정 데이터 셋에서는 트리가 한쪽으로 일렬 형태의 트리가 나올 수도 있다. 시간복잡도는 일반적으로 \(O(h)\)로 나타내는데, 이렇게 극단적인 경우에서의 시간복잡도는 \(O(n)\)의 시간복잡도를 갖는다. 모든 데이터를 통과해야지 삽입, 삭제가 가능하기 때문이다.
반면에 좌우 균형이 알맞은 이진 트리는 h가 \(\log{n}\)을 띄므로 \(O(\log{n})\)의 시간복잡도를 갖는다.
Deletion case (삭제 케이스)
이진 탐색 트리의 삭제 과정은 삭제하는 노드의 조건에 따라 삭제 방식이 바뀌게 된다. 크게 2가지 경우의 케이스로 분류된다.
- 삭제할 노드의 자식 중 하나라도 리프 노드일 때
- 삭제할 노드의 자식이 모두 존재할 때
1번 경우는 처리해주는 것이 어렵지 않다. 삭제노드를 지우고 그 아래 있는 자식을 바로 연결해주면 된다. 문제는 2번 케이스에서 발생된다. 생각보다 해줘야 하는 작업이 많기 때문이다.
2번 케이스가 1번 케이스와 다르게 문제가 발생하는 이유는 간단한데, 1번 케이스는 자신 밑에 자식이 있거나 없기 때문에 자신의 데이터가 후속 데이터에 크게 영향이 미치지 않는다. 하지만 자식이 둘이라는 의미는 후속 데이터가 영향을 받을 수 있다.
자식이 둘인 경우 후속 데이터가 영향을 받는다는 게 무슨 의미냐면 아래와 같다고 생각하면 된다.
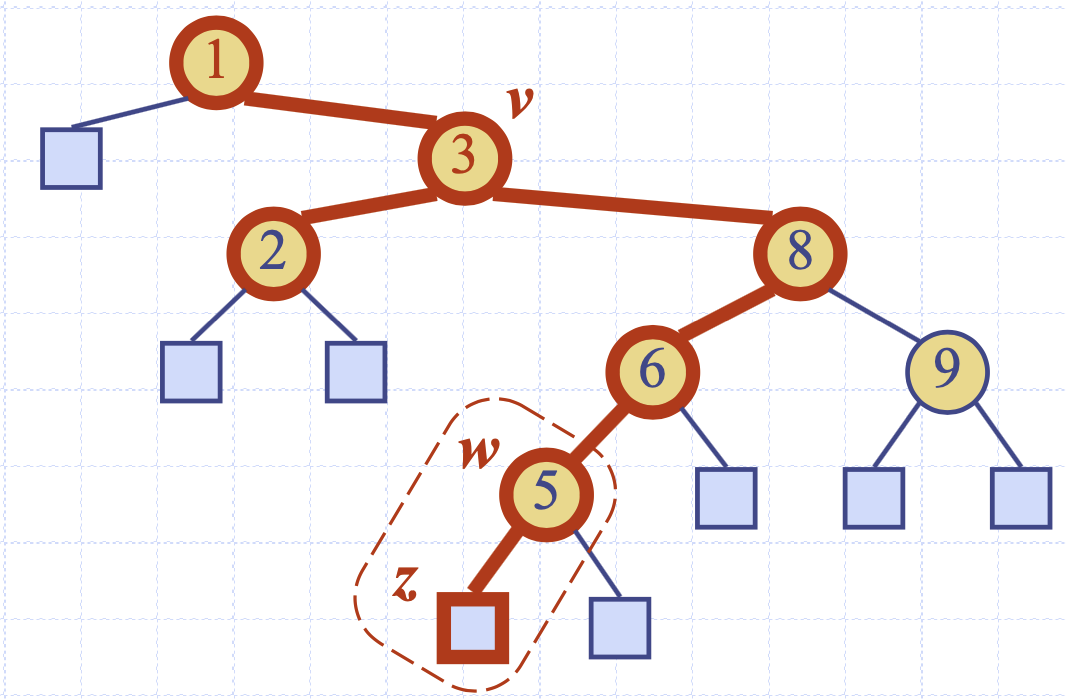
위의 상황처럼 3번 노드를 제거하는 상황이면 단순하게 3번을 제거하고 2번이나 8번을 해당 위치에 대체하면 문제가 발생한다. 8번이 해당 위치를 대체한다면 6번 아래에 있는 모든 노드들은 2번 자식들로 모두 옮겨져야 한다는 문제가 발생한다. 2번을 대체한다고 해도 지금은 문제가 없어 보이지만 2번 아래에 자식이 있다면 똑같은 문제가 발생한다.
그래서 일반적으로 삭제하는 노드들 대체하는 노드는 삭제 노드의 오른쪽 트리 중 가장 작은 값으로 대체한다.
오른쪽 부분 트리의 가장 왼쪽 리프 노드는 이진 탐색 트리의 원리상 삭제 노드와 가장 가까우면서 큰 노드가 되게 된다.
AVL-Tree (균형 잡힌 이진 탐색 트리)
앞서서 말한 시간복잡도 부분에서 완벽하게 \(O(\log{n})\)을 보장하지 못함을 알 수 있다. 이러한 것을 보장하기 위해서 나온 것이 AVL Tree이다. AVL 트리는 항상 양쪽 균형이 최대한 맞춰진 이진 탐색 트리이다.
(참고로 AVL은 사람이름이다.)
이전에 트리에서 노드의 높이를 말한 적이 있는데, 노드의 높이면 해당 노드를 루트 노드로 하는 부분 트리라고 했다. AVL Tree는 자식 노드의 높이차이가 최대 1까지만 나는 경우를 말한다.

부분 트리의 높이를 계산할 때 아래서부터 카운트를 하는데, 리프노드가 1인 이유는 일반적으로 리프노드에 2개의 더미노드가 존재하기 때문이다. 더미노드의 높이를 0이라고 간주한다. 부모노드의 높이는 자식 노드 중 높은 것의 높이 +1을 한 값이 된다. AVL 트리의 이런 성질 height-balance property라고 한다. AVL Tree는 새로운 값이 삽입되거나 삭제되었을 때, height-balance property를 유지를 해야 한다. 그래서 그런 높이를 조정하는 과정이 Trinode Restructuring 또는 Rotation이라고 한다.
Rotation (회전)
회전은 AVL Tree의 각 부분트리들의 높이를 조정해주는 과정에서 사용된다. 회전은 보통 1번이나 2번으로 이루어지고 왼쪽 회전, 오른쪽 회전이라고 부른다. 이런 회전의 조합이 1번이냐 2번이냐에 따라 1번 회전, 2번 회전으로 구분된다.
위의 트리에서 삽입이 이루어진 경우를 한 번 보자.
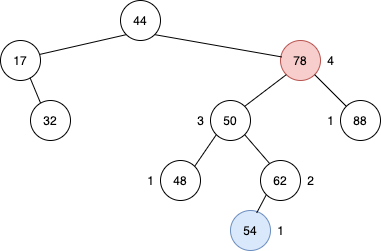
54를 가진 노드가 추가되면서 78 값을 가진 노드에서 높이 밸런스 특성이 깨졌다. 설명의 편의를 위해서 노드의 값을 노드의 이름으로 부르겠다. 78노드의 높이가 4인 이유는 자식의 높이 중 가장 큰 높이+1이 부모의 높이가 되기 때문이다.
AVL Tree는 height-balance property를 유지해야 하므로 회전을 진행한다. 회전을 진행하는 과정에서는 총 3개의 노드가 위치를 바꾸게 되는데, 3개의 노드는 x,y,z라고 지칭한다. 그리고 해당 노드를 정하는 조건은 다음과 같다.
- z노드는 최초로 height-balance가 깨진 노드로 한다. (78노드)
- y노드는 z노드의 자식 중 가장 높이가 높은 노드이다. (50노드)
- x노드는 y노드 중 가장 높이가 높은 노드이다. (62노드)
- 2,3번 과정에서 자식 노드들의 높이가 같으면 보통 왼쪽 노드를 선택한다. 회전의 편의성을 위해서이다.
이렇게 정해진 x, y, z노드에 다시 a, b, c라는 이름을 붙여준다. a, b, c를 붙이는 조건은 중위순회를 기준으로 먼저 중위순회가 이뤄지는 순서로 이름을 붙여준다. 여기서는 y,x,z순서로 a,b,c가 붙여진다.

이렇게 설정된 노드에서 x를 가운데로, y를 왼쪽, z를 오른쪽 자식으로 놓게 설정한다. 그 후에 자식을 크기 순서로 놓아주면된다. 이렇게 위치를 조정하면 아래와 같이 높이 밸런스가 알맞게 조정이 된다.

실제로 이 과정은 이렇게 보면 단순하게 회전이 진행된 것 같지만 2번 회전한 경우에 해당된다. 일반적으로 1번 회전하는 경우는 a, b, c가 일렬로 연결이 된 경우에 해당된다. 위는 a, b, c가 지그재그 형태로 이뤄진 경우로 2번 회전을 진행하게된다. 간단한 회전의 경우를 보면 아래처럼 구분된다고 보면 된다.
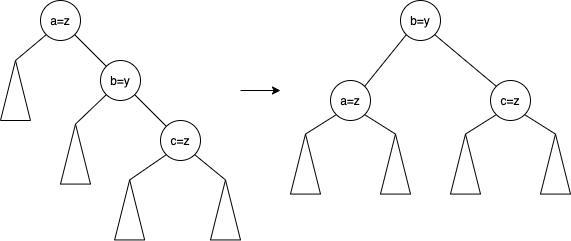
위와 같은 경우는 1번 회전을 진행한 single rotation이라고 한다. 중심이 되는 노드가 b가 되게 만드려면 왼쪽으로 돌려야하므로 왼쪽 회전이라고 한다. 반대의 경우는 오른쪽 회전이라고 한다.
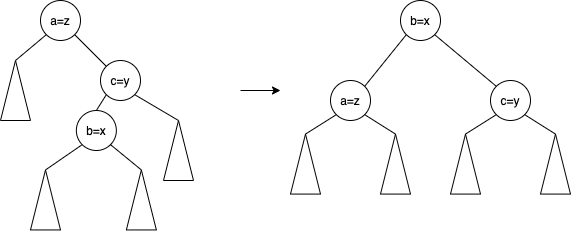
이 경우가 예시로 들었던 2중 회전의 경우이다. 2중 회전은 사실 별 거라고 느낄 필요는 없다. 우선 b와 c를 교체해준다. 그러면 single rotation의 형태를 띄게되는데, 여기서는 일반적인 single rotation처럼 진행해주면 된다.
삭제가 발생했을 경우에도 삽입과 같이 높이들을 조정해주면 된다.
여기서 주의해야할 점이 있는데, 삽입은 height balance가 깨진 노드를 조정해도 그 부모에 영향이 없다. 하지만 제거를 진행하면 height balance를 조정하더라도 부모 노드의 높이에 영향을 끼칠 수 있어서 루트노드까지 모든 hegith balance를 체크해주는 과정을 진행해야한다.
사실 나도 AVL Tree는 너무 어렵다... 이론적으로 대충 이해만 하고 넘어가는 정도...
BST implementation (이진 탐색 트리 구현)
Node prototype
class Node {
private:
Node* parent;
Node* right;
Node* left;
int data;
public:
Node() {
data = NULL;
parent = NULL;
right = NULL;
left = NULL;
}
Node(int data) {
this->data = data;
parent = NULL;
right = NULL;
left = NULL;
}
void insert(Node* child);
int degree();
int depth();
~Node() {}
friend class BST;
};이진 트리에서 한 것처럼 이진 트리의 노드 클래스의 함수들이다. 생성자는 일반적인 이진 트리의 생성자와 동일하다. 여기서 노드의 부모자식 관계를 처리하는 함수인 insert와 트리의 깊이와 자식 수를 반환해주는 함수를 만들었다.
Node insert function
void insert(Node* child) {
if (child->data > data) {
right = child;
child->parent = this;
}else if (child->data < data) {
left = child;
child->parent = this;
}
}노드의 자식을 결정해주는 함수이다. 자식으로 들어오는 노드의 값이 현재 노드보다 크면 오른쪽 자식으로 지정해주고 반대의 경우는 왼쪽 자식으로 지정해준다.
Node degree and depth
int degree() {
int deg = 0;
if (left != NULL) deg++;
if (right != NULL) deg++;
return deg;
}
int depth() {
if (parent == NULL) return;
return parent->depth() + 1;
}degree는 간단하게 자식이 있는 경우를 보고 카운트를 올려주면 된다. depth가 좀 어려운데, 가장 좋은 방법은 재귀함수로 구현해주면 된다. 루트가 0이고 0에서부터 1씩 올려주면서 값을 반환해주면 된다.
BST prototype
class Node {...};
class BST {
private:
Node* root;
public:
BST() {
root = NULL;
}
~BST() {this->treeDestructor(this->root);}
void treeDestructor(Node* temp);
Node* findNode(int data);
Node* findMin(Node* node);
void insert(int data);
void delNode(int data);
void transplant(Node* u, Node* v);
}트리이므로 소멸자를 확실히 진행해줘야한다. findMin과 findNode는 노드를 제거하는 경우에서 활용이 되므로 반드시 만들어줘야한다.
Tree destructor function
void treeDestructor(Node* node) {
if (node == NULL) return;
if (node->right != NULL) treeDestructor(node->right);
if (node->left != NULL) treeDestructor(node->left);
delete node;
}트리를 제거하는 함수이다. 기본적인 원리는 dfs의 형식으로 가장 안쪽의 리프노드부터 제거해준다. 그렇게 제거해주면서 모든 노드를 제거한다.
Find node function
Node* findNode(int data) {
Node* node = root;
while (node != NULL) {
if (node->data == data)
return node;
else if (node->data < data)
node = node->right;
else
node = node->left;
}
return NULL;
}나름 가독성을 신경썼는데 별로 좋은거 같진 않다....
반복문의 이동은 현재 노드가 더미에 도달한 상황에서 종료시킨다. 리프가 더미에 도달했다는 의미는 찾고자하는 노드가 없다는 의미이므로 해당 노드가 없다는 의미로 NULL을 반환해준다. 찾는 노드를 찾았다면 해당 노드를 반환해주면된다.
Find min node function
Node* findMin(Node* node) {
Node* tmp = node;
while (tmp->left != NULL) {
tmp = tmp->left;
}
return tmp;
}주어진 노드를 루트로 하는 부분 트리의 최소 노드를 찾아낸다. 방법은 이진 탐색 트리 원리를 활용하면된다. 현재 루트부터 가장 왼쪽으로 계속 이동하면된다.
Insert function
void insert(int data) {
Node* newNode = new Node(data);
if (root == NULL) {
root = newNode;
}else{
Node* tmp = root;
while (1) {
if (tmp->data < data) {
if (tmp->right == NULL) break;
tmp = tmp->right;
}else if (tmp->data > data) {
if (tmp->left == NULL) break;
tmp = tmp->left;
}
}
tmp->insert(newNode);
}
}새로운 값을 삽입하는 함수이다. 들어갈 위치가 반드시 있으므로 들어갈 위치를 찾으면 반복을 멈춰준다. 반복이 종료된 이후에는 노드에 있는 삽입함수로 노드를 연결해주면된다.
Delete and transplant function
void transplant(Node* u, Node* v) {
if (u->parent == NULL) {
this->root = v;
}else if (u == u->parent->left) {
u->parent->left = v;
}else {
u->parent->right = v;
}
if (v != NULL)
v->parent = u->parent;
}
void delNode(int data) {
Node* tmp = findNode(data);
if (tmp->left == NULL) {
transplant(tmp, tmp->right);
}else if (tmp->right == NULL) {
transplant(tmp, tmp->left);
}else {
Node* min = findMin(tmp->right);
if (min->parent != tmp) {
transplant(min, min->right);
min->right = tmp->right;
min->right->parent = min;
}
transplant(tmp, min);
min->left = tmp->left;
min->left->parent = min;
}
}transplant함수는 이름처럼 자식을 삭제노드의 부모에 이식하는 함수이다. if문과 else if문까지는 deletion case1에 해당하는 자식이 1개이거나 없는 경우에 시행된다.
가장 까다로운 부분이 else인 deletion case2에 해당된다. 우선 가장 작은 노드를 저장해주고 기존에 말했던 방식처럼 삭제를 진행해주면 된다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [Data Structure] DFS (깊이 우선 탐색) (0) | 2021.06.24 |
|---|---|
| [Data Structure] Graph (그래프) (0) | 2021.06.24 |
| [Data Structure] Hash (해시) (0) | 2021.06.24 |
| [Data Structure] Priority Queue (우선순위 큐) (0) | 2021.06.24 |
| [Data Structure] Binary Tree (이진트리) & Tree 구현 (0) | 2021.06.24 |