[Data Structure] Graph (그래프)
Graph (그래프)
그래프란 정점과 간선으로 구성된 자료구조이다. 일반적으로 G = (V,E)로 나타내는데, V는 vertices로 정점을 말하고, E는 edges인 간선을 의미한다. |V|는 정점의 개수를 의미하고 |E|는 간선의 개수를 의미한다.
그래프는 간선의 종류에 따라 2가지로 구분할 수 있다. 그리고 그 종류에서도 그래프의 특징으로 종류를 더 세분화할 수 있다.
그래프의 종류
그래프는 간선의 종류로 크게 2가지로 나눠지게 된다.
- 무향 그래프 (undirected graph)
- 유향 그래프 (directed graph)
명칭에서 보이듯이 그래프의 간선에 방향성이 있고 없고의 차이를 보여준다.
무향 그래프 (undirected graph)

그래프의 이름 그대로 간선에 방향성이 존재하지 않는다. 그래서 1에서 4, 4에서 1의 이동이 모두 가능한 그래프이다. 그래프의 간선을 표시할 때 보통 (1, 4)와 같이 표시하는데, 이 과정에서 순서가 정해지지 않은 pair가 된다. 즉 무향 그래프에서는 (1,4)나 (4,1)이나 같은 간선을 말한다.
유향 그래프 (directed graph)

그림이 커져보이는 거는 기분 탓이다
간선에 방향성이 생긴 그래프다.이 그래프는 무향 그래프와 다르게 (1,4)와 (4,1)은 서로 다른 간선을 나타내게 된다. 간선이 방향성을 갖기 때문에 순서가 곧 방향성을 나타내기 때문이다. 그래서 유향 그래프는 순서가 정해진 pair가 된다.
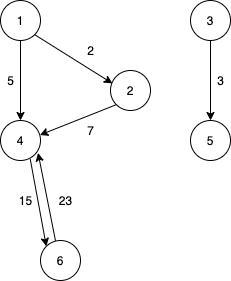
일반적으로 무향 그래프보다는 유향 그래프에서 자주 쓰이는 추가적인 그래프의 옵션이 있는데, 그래프의 간선에 가중치가 존재하는 경우를 가중치 그래프라고 한다. 가중치 그래프에서 가중치는 보통 이동할 때 걸리는 시간, 비용등으로 대표가 되어서 최단거리, 최소비용으로 이동하는 경로를 찾을 때 사용된다.
그래프 용어
그래프에서 사용되는 용어가 몇가지가 존재한다.
- 인접 정점 (adjacent vertices)
- 차수 (degree)
- 사이클 (cycle)
인접 정점 (Adjacent Vertices)
그래프의 인접한 정점이란 말 그대로 특정 정점에서 직접적으로 갈 수 있는 정점들을 말한다.
보통 인접정점들을 묶어 놓은 것을 level이라고 한다.

1번 정점의 인접 정점은 2, 4가 있고 2의 인접 정점은 3, 4와 같이 있다. 이렇게 인접 정점을 아는 이유는 그래프를 만드는 방법을 결정하는 것에도 관련이 깊다. 이런 인접 정점들의 개수를 차수라고 한다. 차수를 계산하는 방법은 무향 그래프와 유향 그래프에 따라 다르다.
차수 (degree)
우선적으로 차수를 계산하기 쉬운 그래프인 무향 그래프를 설명해보면, 무향 그래프는 말 그대로 그냥 인접한 정점 개수를 세면된다. 위에 있는 그래프를 기준으로 설명하면 1번 정점의 차수는 2가 되게 된다.
이게 유향 그래프로 가면 고려해야할 것이 생긴다. in-degree와 out-degree를 따로 구해서 그 두 degree를 합친 것이 총 차수가 되게 된다.

4번 정점을 기준으로 설명해보면 4번 정점의 in-degree는 3이다. 1, 2, 6번 정점으로부터 들어오는 간선이 있기 때문이다. out-degreesms 1이 된다. 6번 정점으로 나가는 간선이 있기 때문이다. 그래서 4번 정점의 총 차수는 3 + 1인 4가 된다. 단순하게 차수만 계산한다면 무향 그래프와 원리는 같지만 그 차수를 구성하는 종류가 2가지로 나뉘는 것을 생각해볼 필요가 있다.
사이클 (cycle)
사이클이란 그래프의 부분을 보는 게 아니라 전체적인 그래프의 이동 경로를 봤을 때 나타난다.
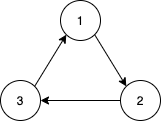
전체적인 경로를 봤을 때, 경로가 순환이 발생하면 그 경우를 사이클이라고 한다. 이런 사이클이 발생을 하는 게 자연스럽고 큰 문제는 아니지만 알고리즘 중 벨만-포드 알고리즘과 같은 최적 경로 판단 문제에서는 사이클이 문제 요소가 될 수 있다. 그래서 이런 사이클을 확인하는 게 중요하다.
나중에 DFS나 BFS문제를 풀 경우 사이클을 하나의 묶음으로 처리하여 사이클의 수를 확인해야하는 문제들도 있으므로 사이클 확인은 중요한 정보가 된다.
구현 방법
그래프의 구현 방법은 총 3가지가 있다.
- 간선 리스트
- 인접 리스트
- 인접 행렬
이렇게 3가지 종류로 구현이 가능하다. 보통 알고리즘 문제를 풀 때는 편의를 위해서 인접 리스트와 인접 행렬 방식을 많이 사용한다. 실제로 간선 리스트 방식은 좀 오래된 그래프 표현 방식이다.
그래프를 구현할 때 막상 구현하려고 하면 어떻게 해야 구현이 가능한지가 감이 안 잡힐 수 있다. 그래프의 구현은 생각보다 간단하다. 그래프의 구성은 정점과 간선이지만 우리가 실제로 그래프로 인식하는 이유는 간선이 생성되기 때문이다. 즉 그래프를 구성할 때는 간선을 저장하면 그것이 결국 그래프가 되는 것이다.
아래의 그래프를 기준으로 각 구현방법을 설명해보겠다.
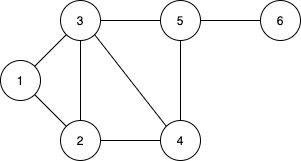
간선 리스트 (Edge List)

간선 리스트방식은 말 그대로 모든 간선의 종류를 저장하는 방식이다. 각 정점의 차수를 저장하는 배열이 존재하고 각 간선을 저장하는 배열도 존재하게 된다. 이 방식을 잘 활용하지 않는 이유는 우선적으로 다른 두 방식에 비해서 메리트가 떨어지기 때문이다.
인접 리스트 방식은 간선 리스트보다 시간 복잡도 측면에서 유리한 메리트를 갖고 인접행렬은 공간 상의 낭비가 존재하지만 직접적으로 간선들을 컨트롤 할 수 있다는 장점이 있다.
인접 리스트 (Adjacency List)

알고리즘 문제를 풀 때 인접 행렬 방식과 유사한 빈도로 많이 쓰는 방식이다. 메모리 낭비를 줄이기 위해서 사용하는 방식이다. 일반적으로 간선이 별로 없는 희소 그래프(Sparse graph)에서 자주 사용된다. 직접적으로 특정 정점간의 연결관계를 파악하는 것보다 전체적인 연결 흐름을 파악하는 것을 주요 요구로 할 때 많이 사용된다.
구현 방식은 2차원 배열로 만든다. 각 첫번째 배열의 인덱스가 정점들을 나타내고 각 인덱스 별로 2번째 배열에는 그 정점과 연결된 다른 정점의 이름을 저장한다.
자세한 구현은 그래프 직접구현에서 설명하겠다.
인접 행렬 (Adjacency Matrix)
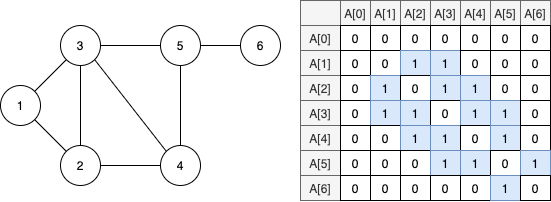
인접 행렬은 모든 정점을 2차원 배열로 만들고 저장한다. 그리고 간선의 연결 정보를 좌표로 표시해서 저장한다. 모든 정점의 순서쌍을 만들어서 저장하므로 \(O(V^2)\)의 공간복잡도를 갖는다. 따라서 상당히 많은 메모리를 차지하므로 너무 많은 정점을 갖는 그래프에서는 잘 사용하지 않는다. 하지만 특정 간선을 확인해야하는 경우에서 굉장히 빠른 속도를 보여준다.
인접 리스트는 최악 수행시간이 \(O(n)\)의 시간을 갖지만 인접 행렬은 특정 연결관계 확인에 무조건 \(O(1)\)시간이 발생한다.
공간적인 소모가 크므로 보통 정점의 개수와 간선의 개수가 유사한 밀집 그래프(Dense graph)에서 자주 사용된다.
Graph implementation (그래프 구현)
그래프 구현은 간선 리스트는 자주 활용하지 않으므로 생략하고 인접 리스트 방식만 설명하겠다.
인접 행렬은 그냥 단순히 정적 2차원 배열로 만들면 된다.
Adjacency List Graph
Graph prototype
#include <vector>
#include <iostream>
using namespace std;
class Graph() {
private:
int N;
vector<vector<int>> adj_list;
public:
Graph() {
N = 0;
}
Graph(int n) {
N = n + 1;
adj_list.resize(N);
}
void addEdge(int u, int v);
int degree(int u);
};그래프에 필요한 함수는 그렇게 많지 않다. 물론 전체를 다 리스트로 구현하면 좀 더 복잡하지만 벡터는 일종의 리스트 역할을 할 수 있으므로 벡터로 대신할 수 있다.
벡터는 정점과 그 정점이랑 연결된 정점들을 저장하는 역할을 할 것이다. 중요한 점은 기본적으로 벡터에 정점의 개수만큼 정확하게 벡터 크기를 resize해준다.
참고로 이 그래프는 무향 그래프를 기준으로 설명한다.
add edge function
void addEdge(int u, int v) {
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}각 벡터의 정점 위치에 연결 정점을 저장해준다. 이는 무향 그래프 기준으로 만들경우 값을 바꿔서 한번 더 저장해주는 것이고 유향 그래프인 경우 한 번만 저장해주면 된다.
degree function
int degree(int u) {
return adj_list[u].size();
}특정 정점의 차수는 해당 정점을 저장한 인접 리스트의 크기만큼을 반환해주면 된다. 인접 리스트의 원리를 알면 간단한 것이다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [Data Structure] BFS (너비 우선 탐색) (0) | 2021.06.25 |
|---|---|
| [Data Structure] DFS (깊이 우선 탐색) (0) | 2021.06.24 |
| [Data Structure] Binary Search Tree (이진 탐색 트리) (0) | 2021.06.24 |
| [Data Structure] Hash (해시) (0) | 2021.06.24 |
| [Data Structure] Priority Queue (우선순위 큐) (0) | 2021.06.24 |