[Data Structure] DFS (깊이 우선 탐색)
그래프 탐색 (Graph Search)
앞서서 그래프를 배웠다. 트리에 트리를 탐색하는 트리 순회가 있었다면, 그래프는 그래프 탐색이 존재한다. 그래프 탐색 방법에는 DFS와 BFS가 존재한다.
이번 글에서는 DFS에 대해서 이야기할 예정이다.
그래프 탐색을 배우는 이유는 그래프의 이동 경로나 생김새를 파악하기 위해서 사용한다. 탐색을 통해서 그래프에 사이클이 몇개고, 전체적인 묶음이 몇개인지 알 수 있기때문이다.
DFS VS BFS
DFS는 깊이 우선 탐색(Depth-First-Search)의 약자이고 BFS는 너비 우선 탐색(Bredth- First-Search)의 약자이다. 이름에 탐색 방식이 들어가 있다. DFS는 깊게 들어가는 것을 우선으로 하는 탐색방식이고 BFS는 넓은 분포, 즉 한 level씩 탐색을 하는 방식이다.
단순히 탐색만을 한다면 어떤 방식을 써도 상관없지만 특정 경우를 필요로하면 상황에 따라서 DFS와 BFS를 선택해야한다.
우선 BFS는 최단 경로를 찾을 때 사용한다. 일반적인 그래프는 가중치가 없으므로 BFS로 최단경로를 찾을 수 있고 가중치가 존재하는 가중치 그래프에서는 BFS를 변형하는 다익스트라(Dijkstra) 알고리즘을 사용하면 최단 경로를 찾을 수 있다.
이렇게 BFS는 사용처가 명확한데, DFS는 사용처가 약간 불분명하다고 느껴질 수 있다. 사실 DFS는 BFS에 비해 코딩이 직관적이라 그래프 뿐만 아니라 경로 찾기 문제를 풀 때 자주 사용한다. (최단경로가 아닌 단순 경로) 하지만 명확하게 DFS가 사용되는 곳을 말하면 백트래킹(Backtracking) 에서 자주 사용된다. 백트래킹은 특정 경우의 수를 찾기 위해 불가능한 경우의 수를 가지치기 해야하므로 하나의 방식을 끝까지 확인하면서 가능성을 파악해야한다. 그렇기 때문에 DFS 방식을 사용한다.
이 글은 알고리즘 글이 아니라 자세히 설명하지는 않겠다.
Depth-First-Search(깊이 우선 탐색)란?
DFS의 원리를 간단하게 설명하면 한 우물 파기 이다. 우물의 끝을 볼 때까지 그 우물만 파는 방식이다. 그렇기 때문에 그 우물이 끝이 있어야만 탐색이 끝나고 끝이 없을 수도 있다면 DFS를 사용하면 안된다. 그래프를 가지고 DFS방식을 설명해보겠다.

전반적으로 트리처럼 생겼지만 트리는 그래프의 특수한 경우를 트리라고한다. 그래서 위의 트리같이 생긴 그래프를 탐색한다고 보면 보통 시작 정점을 주는데 일반적으로 1번 정점이나 0번 정점을 시작 정점으로 설정한다. 전체적인 탐색 방식은 트리의 전위순회 방식과 같다고 생각하면 편하다.
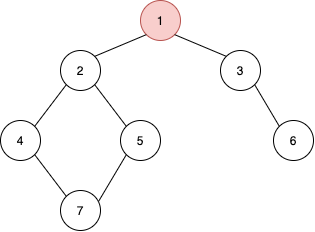
1번 정점을 탐색을 완료 했다면 현재 정점의 인접하는 정점들을 확인한다. 탐색 순서를 작은 숫자를 우선으로하면 다음 탐색 위치는 2번 정점이 된다. 이제 2번 정점을 탐색하게 된다.

2번 정점에 들어오게 되면서 2번 정점을 탐색한다. 현재 정점 탐색이 완료되었으므로 현재 정점의 인접 정점들을 확인한다. 인접 정점에는 1번과 4번, 5번 정점이 있다. 여기서 1번 정점은 이미 탐색을 했으므로 1번 정점으로 탐색방향을 잡으면 안된다. 그래서 4번과 5번 중 하나로 탐색 방향을 잡게된다. 작은 정점으로 탐색하므로 4번 정점으로 탐색한다.

4번 정점으로 들어왔다. 이제 인접 정점으로 탐색을 진행하는데, 2번과 7번 중 탐색을 하지 않은 7번 정점으로 이동한다.

7번 정점 탐색을 마쳤다. 7번 정점의 인접정점 중에서 탐색을 하지 않은 정점은 5번 정점이 되게 된다. 5번으로 탐색을 하게된다.

여기서부터가 가장 중요하다. 5번 정점까지 탐색이 끝났다. 5번 정점의 인접 정점에서는 더 이상 방문할 수 있는 정점이 없다. 이 경우에는 바로 이전에 탐색한 정점으로 이동 한다. 만약 이전에 탐색한 정점에도 방문 가능 정점이 없으면 방문이 가능한 경우가 나올 때까지 반복해서 돌아간다. 5->7->4->2->1로 가게 되면 1번 정점에서는 인접 정점으로 이동이 가능하게 된다. 1번 정점의 인접 정점 중 탐색하지 않은 3번 정점으로 이동하자.

3번 정점 탐색이 끝났다. 이전 방식과 동일하게 인접 정점 중 탐색하지 않은 정점으로 이동하자.

6번 정점까지 탐색이 되었다. 인접 정점에서 탐색이 가능한 정점이 없으므로 이전처럼 바로 전에 탐색한 정점으로 돌아간다. 끝까지 탐색할 수 있는 정점이 없다면 탐색을 종료하게 된다.
전체적으로 DFS를 모아서 보면 아래와 같이 탐색을 한다.

DFS의 예시
DFS는 미로탐색에서 길 찾기 방식에서 사용된다.

시작에서 미로찾기를 수행하다가 막다른 길을 만날 때까지 해당 경로를 탐색하는 것이다.
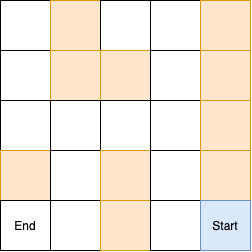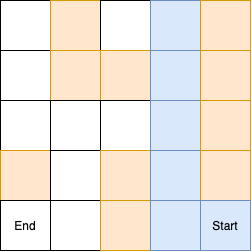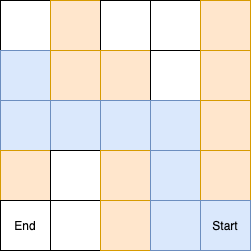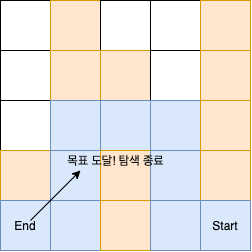
사진에서는 직관적으로 잘 보이기 위해서 방문 경로를 지웠는데, 실제로는 visit이 false가 되는 것이 아니라 갈림길이 나올 때까지 재귀를 탈출하게된다.
DFS implementation (DFS 구현)
DFS 구현을 위한 class를 만들면 아래와 같이 만드는데, 사실 실전에서 Problem solving(알고리즘 문제풀이)을 할 때는 아래처럼 풀지 않는다. 우선 이론적 코딩으로 설명을 하고 2가지 방식의 실전적 코딩을 알려주겠다.
Class coding
Graph making & prototype
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
class Graph() {
private:
int N;
vector<vector<int>> adj_list;
vector<bool> visit;
public:
Graph() {
N = 0;
}
Graph(int n) {
N = n + 1;
adj_list.resize(N);
visit.resize(N);
}
void sortGraph() {
for(int i = 0; i < N; i++)
sort(adj_list[i].begin(), adj[i].end());
}
void addEdge(int u, int v) {
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}
void dfs();
void dfs(int curr);
};그래프 만드는 함수는 이전 글에서 그대로 가져왔다. dfs함수가 2가지가 있는데, 파라미터가 없는 함수는 dfs 시작 함수이고 파라미터가 있는 함수는 실제로 dfs를 수행하는 함수이다. 전위순회와 동일한 방식으로 돌아가므로 재귀함수로 구현을 할 수 있다.
private에 visit이라는 bool타입 변수를 만들어준다. 이 배열의 역할은 해당 정점의 방문여부를 결정해준다. 그래서 그래프 생성과 동시에 N의 크기로 만들어준다.
DFS function
void dfs() {
fill(visit.begin(), visit.end(), false);
dfs(1)
}
void dfs(int curr) {
visit[curr] = true;
cout << "Vertex " curr << " visit\n";
for(int i = 0; i < adj_list[curr].size(); i++) {
int next = adj_list[curr][i];
if (!visit[next])
dfs(next);
}
}파라미터가 없는 dfs시작 함수의 역할은 방문여부를 결정하는 visit벡터를 미방문(false)으로 초기화해준다.
그리고 여기서는 1번 정점을 시작 정점으로 해서 1을 넣었지만 실제로는 저 부분은 시작 정점에 맞춰서 진행한다.
실제로 dfs를 수행하는 함수의 시작은 현재 정점을 방문으로 바꿔주는 것이다. 그 후 해당 정점에 연결된 정점들을 돌면서 탐색을 진행해준다. 여기서 조건문으로 방문이 이뤄지지 않은 정점만 dfs 재귀를 수행해준다.
여기까지가 이론적 부분이고 이제부터는 실전적 부분 설명이다. 관심없으면 이 밑은 읽지 않아도 괜찮다.
Problem Solving Coding
위의 class 방식은 앞서서 말했지만 실전 알고리즘 문제에서는 잘 사용하지 않는다. 실전 알고리즘 문제는 방식에 따라서 크게 2가지 방식으로 코딩을 하는데, 이건 문제에서 그래프를 어떤 방식으로 주어지냐에 따라 코딩 방식이 바뀐다.
위 문제는 인접리스트 방식으로 그래프를 구현하는 경우에 해당하는 문제이다. 인접행렬로 구현해도 괜찮지만 인접리스트로 하는 것이 좀 더 편할 수 있다.

위 문제처럼 특정한 지도(map)를 주는 방식은 인접행렬로 구현하는 것이 유리하게 된다. 위에서 언급한 미로찾기 방식처럼 탐색을 하기에 굉장히 편한 그래프 형태이다.
인접리스트 풀이 코드
#include <vector>
#include <iostream>
using namespace std;
vector<vector<int>> map;
vector<bool> visit;
int N, M; // 전체 정점 개수, 전체 간선 수
void dfs(int curr) {
visit[curr] = true;
cout << "Visit " << curr << " vertx\n";
for(int i = 0; i < map[curr].size(); i++) {
int next = map[curr][i];
if (!visit[next])
dfs(next);
}
}
int main() {
cin >> N;
// 시작 정점이 1인 경우로 설정
map.resize(N + 1);
visit.resize(N + 1);
for (int i = 0; i < M; i++) {
int u, v;
cin >> u >> v;
map[u].push_back(v);
map[v].push_back(u);
}
dfs(1);
}이미 앞서서 이론적으로 설명한 기반이 인접리스트라 코드는 동일하다. 단지 문제풀이때는 전역변수로 설정해서 모든 값이 정수는 0으로, bool타입은 false로 자동 초기화가 된다.
인접행렬 풀이 코드
#include <iostream>
#include <utility>
#include <vector>
using namespace std;
typedef pair<int> P; // x, y 좌표 저장
vector<P> start;
int dirx[4] = {-1, 1, 0, 0};
int diry[4] = {0, 0, -1, 1};
bool map[1001][1001];
bool visit[1001][1001];
int N; // 전체 정점 개수, 전체 간선 수
void dfs(int x, int y) {
visit[x][y] = true;
cout << "x : " x << " , y : " << y << " visit \n";
for (int i = 0; i < 4; i++) {
int nx = x + dirx[i];
int ny = y + diry[i];
if (nx >= 0 && nx <= N && ny >= 0 && ny <= N) {
if (!visit[nx][ny])
dfs(nx, ny);
}
}
}
int main() {
int u, v;
// 시작 정점 역할
cin >> N;
// N x N 행렬로 만든다고 가정한다.
// map이 입력으로 주어질 때로 가정
for (int i = 0; i < N; i++) {
for (int i = 0; i < N; i++) {
int curr;
cin >> curr;
// 보통 입력은 1, 0으로 주어진다.
map[i][j] = curr;
}
}
cin >> u >> v;
dfs(v, u);
}
인접행렬 방식의 그래프는 필요한 변수가 여러 개가 존재한다. 좌표의 형식으로 경로를 저장하기 때문에 좌표를 이동해주는 변수가 필요하다. 그 변수가 바로 dirx와 diry의 역할이다. 위의 코드처럼 단일 배열 2개로 만들어도 괜찮고 2차원 배열로 만들어도 괜찮다. 이동 방향이 4방향이냐 8방향이냐에 따라 배열의 이동 좌표를 확장해주면 된다.
보통 visit을 건들 때 일반적으로 말하는 x,y의 위치가 배열에서 나타내는 순서와 반대로 말하므로 헷갈리지 않게 조심해야한다. 특히 dfs 내부에서 첫번째 if문의 역할인, 다음에 이동하는 좌표가 탐색을 요구하는 범위 내에 있는 지를 확인하는 상항에서 out of range 에러를 일으킬 수 있다. 그래서 헷갈리지 않게 주의해줘야한다.
그 외의 방식은 좌표를 이동하면서 일반적인 dfs와 유사하게 방식을 진행하면된다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [Data Structure] BFS (너비 우선 탐색) (0) | 2021.06.25 |
|---|---|
| [Data Structure] Graph (그래프) (0) | 2021.06.24 |
| [Data Structure] Binary Search Tree (이진 탐색 트리) (0) | 2021.06.24 |
| [Data Structure] Hash (해시) (0) | 2021.06.24 |
| [Data Structure] Priority Queue (우선순위 큐) (0) | 2021.06.24 |